6. Sınıf Matematik Ders Kitabı 38-39-40-41-42-43-44-45-46-47. Sayfa Cevapları 1. KİTAP

6. Sınıf Matematik Ders Kitabı 38-39-40-41-42-43-44-45-46-47. Sayfa Cevapları 1. KİTAP 2025-2026 eğitim-öğretim yılı konusu içerisinde 6. sınıf öğrencilerinin en çok ihtiyaç duyabileceği konular arasında bulunan ve içerisinde Asal Sayılar Etkinliği Cevapları konusunun bulunduğu 6. Sınıf Matematik Ders Kitabı Sayfa 38-39-40-41-42-43-44-45-46-47 Cevapları konusunu paylaştık. Cevaplarla ilgili görüş ve önerilerinizi yorumlardan yazarak bildirebilirsiniz.
6.Sınıf MEB Yayınları Matematik Ders Kitabı 38-39-40-41-42-43-44-45-46-47. Sayfa Cevapları 1. KİTAP Asal Sayılar
- 6. Sınıf Matematik Ders Kitabı Sayfa 38 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 39 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 40 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 41 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 42 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 43 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 44 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 45 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 46 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 47 Cevapları MEB Yayınları
6. Sınıf Matematik Ders Kitabı Sayfa 38 Cevapları MEB Yayınları
Etkinlik 1: Bilgi Hayat Kurtarır

Buna göre aşağıdaki soruları cevaplayınız.
1) 2, 3, 5 ve 7 sayılarının çarpanları ile ilgili neler söyleyebilirsiniz?
Cevap: Bu sayılar yalnızca 1’e ve kendilerine bölünebilirler.
2) 1 m² yi temsil eden kareler kullanarak bu bölümlerin zeminlerinin olası şekillerini örnekteki gibi modelleyiniz.
Cevap.
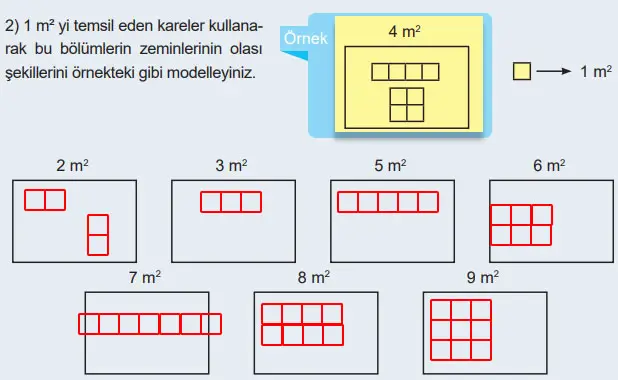
3) Bazı zeminleri modellerken kareleri tek sıra hâlinde dizmekten başka bir seçeneğinizin olmadığını fark ettiniz mi? Bu zeminleri modellerken tek seçeneğinizin olmasının nedenini arkadaşlarınızla tartışınız.
Cevap: Bölenleri yalnızca 1 ve kendisi olan sayılar tek sıra oldu.
6. Sınıf Matematik Ders Kitabı Sayfa 39 Cevapları MEB Yayınları
Etkinlik 2: Erathosthenes Kalburu
1. Adım: En küçük asal sayı 2 olduğundan 2’yi işaretleyiniz. Daha sonra 2’nin katlarının üzerini çiziniz.
Cevap:
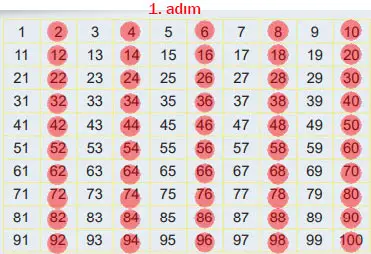
2. Adım: 3 asal sayı olduğu için 3’ü işaretleyiniz. Daha sonra 3’ün katlarının üzerini çiziniz.
Cevap:
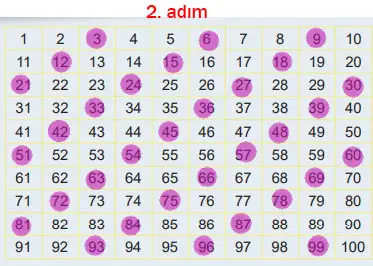
3. Adım: 5 asal sayı olduğu için 5’i işaretleyiniz. Daha sonra 5’in katlarının üzerini çiziniz.
Cevap:
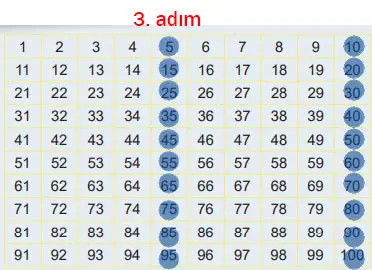
4. Adım: 7 asal sayı olduğu için 7’yi işaretleyiniz. Daha sonra 7’nin katlarının üzerini çiziniz.
Cevap:
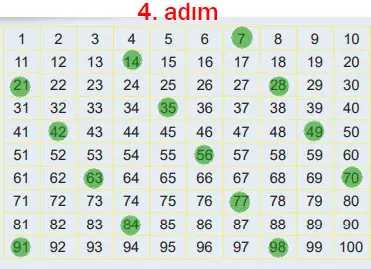
5. Adım: 1 dışında üzeri çizilmemiş sayıları işaretleyiniz
Cevap:
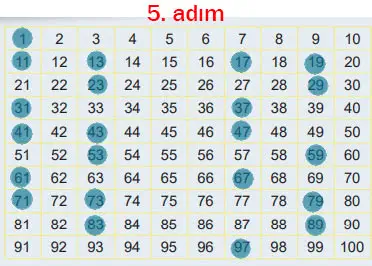
Sınıfınızda gruplar oluşturup aşağıdaki soruları cevaplayınız. Fikirlerinizi diğer gruplarla paylaşarak tartışınız.
1) 1, neden asal sayı değildir?
Cevap: Asal sayılar 1 ve kendisine bölünebilen 1’den büyük sayılar anlamına geldiği için 1 bu tanıma giremez.
Bunun sebebi asal sayıların temel özelliğinin, sadece iki farklı pozitif böleni olmasıdır. 1’in kendinden başka böleni olmadığı için sadece 1 pozitif böleni var demektir.
2) 2’den başka çift asal sayı var mıdır?
Cevap: 2’den başka asal sayı yoktur. 2 dışındaki tüm çift sayılar 2’ye bölünebileceği için asal sayı tanımına uyamazlar.
3) Sizce asal sayıların sonu var mıdır?
Cevap: Sayılar sonsuza kadar devam edeceği için asal sayılarında sonu yoktur, sayı ne kadar büyümeye devam ederse etsin mutlaka asal sayı olan bir sayıya denk gelecektir.
6. Sınıf Matematik Ders Kitabı Sayfa 40 Cevapları MEB Yayınları
Etkinlik 3: Evet – Hayır
Buna göre aşağıdaki soruları cevaplayınız.
1) Bu oyunda tüm arkadaşlarına “EVET” cevabı veren öğrenciye ait karttaki sayıyı belirleyiniz.
Cevap: 1 numaralı kartın sahibi tüm arkadaşlarına “EVET” demiştir.
2) En fazla “HAYIR” cevabı alan öğrenciye ait karttaki sayıyı belirleyiniz.
Cevap: 23 numaralı kart en fazla “HAYIR” demiştir.
3) Sadece bir tane “EVET” cevabı alan öğrencilere ait kartlardaki sayıları belirleyiniz.
Cevap: 2, 3, 5, 7, 11, 13, 17, 19 ve 23 numaralı kartlar bir kez “EVET” cevabı aldı.
6. Sınıf Matematik Ders Kitabı Sayfa 41 Cevapları MEB Yayınları
Örnek 1
Zehra, kareli zemin üzerinde kenar uzunlukları birim cinsinden asal sayı ve alanı 20 br² ile 30 br² arasında olacak şekilde dikdörtgenler oluşturacaktır.
Zehra’nın oluşturabileceği dikdörtgenleri çizerek dikdörtgenlerin çevre uzunluklarını birim cinsinden hesaplayınız.
Cevap:
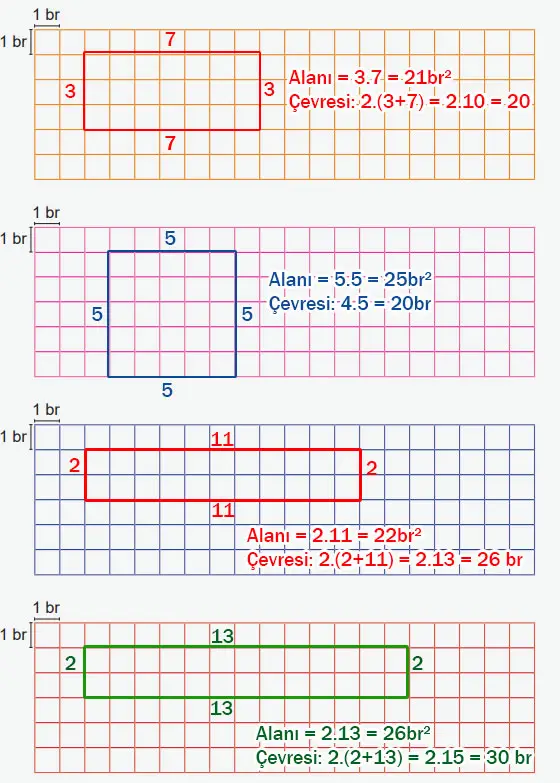
6. Sınıf Matematik Ders Kitabı Sayfa 42 Cevapları MEB Yayınları
Örnek 2
12 – 25
35 – 44
Yavuz Öğretmen’in tahtaya yazdığı doğal sayılar yanda verilmiştir.
Buna göre aşağıdaki soruları cevaplayınız.
a) Yavuz Öğretmen’in yazdığı doğal sayıların çarpanlarını örnekteki gibi belirleyiniz.
Cevap:
12’nin çarpanları: 1, 2, 3, 4, 6 ve 12
25’in çarpanları: 1, 5, 25
35’in çarpanları: 1, 5, 7, 35
44’ün çarpanları: 1, 2 ,4, 11, 22, 44
b) Bu doğal sayıların çarpanlarından asal sayı olanları örnekteki gibi belirleyiniz.
Cevap:
12’nin çarpanlarından asal sayı olanlar: 2 ve 3
25’in çarpanlarından asal sayı olanlar: 5
35’in çarpanlarından asal sayı olanlar: 5 ve 7
44’ün çarpanlarından asal sayı olanlar: 2 ve 11
6. Sınıf Matematik Ders Kitabı Sayfa 43 Cevapları MEB Yayınları
Etkinlik 4: Asal Çarpan Belirleme Yöntemler
Doğal sayıların asal çarpanlarını belirlemeye çalışan iki öğrencinin aralarında geçen diyalog aşağıda verilmiştir.
İki yöntemde de belirlenen asal sayılar başta verilen doğal sayının asal çarpanları olduğuna göre aşağıdaki soruları cevaplayınız.
1) Aşağıdaki çarpan ağacı yöntemi ile ilgili örneği inceleyiniz. Verilen doğal sayıların asal çarpanlarını belirleyiniz ve altlarındaki boşluklara yazınız.
Cevap:
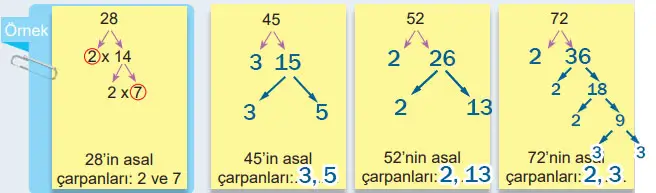
6. Sınıf Matematik Ders Kitabı Sayfa 44 Cevapları MEB Yayınları
2) Aşağıdaki asal çarpan algoritması yöntemi ile ilgili örneği inceleyiniz. Verilen doğal sayıların asal çarpanlarını belirleyiniz ve altlarındaki boşluklara yazınız.
Cevap:
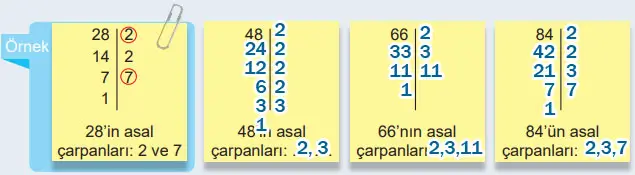
3) Aşağıdaki çarpan ağacı yöntemi ile ilgili örneği inceleyiniz. Verilen doğal sayıları asal çarpanlarının çarpımı şeklinde yazınız.
Cevap:
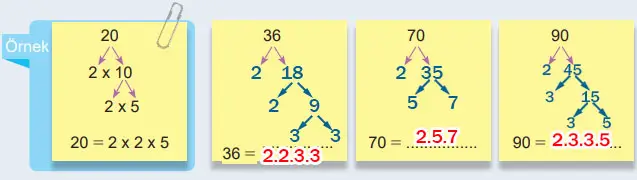
4) Aşağıdaki asal çarpan algoritması yöntemi ile ilgili örneği inceleyip verilen doğal sayıları asal çarpanlarının çarpımı şeklinde yazınız.
Cevap:

5) 1’den büyük doğal sayılardan hangileri asal sayıların çarpımı şeklinde yazılabilir? Düşüncelerinizi arkadaşlarınızla paylaşarak tartışınız.
Cevap: 1’den büyük bütün doğal sayılar, asal sayıların çarpımı şeklinde yazılabilir.
6. Sınıf Matematik Ders Kitabı Sayfa 45 Cevapları MEB Yayınları
Örnek 3
5▇ iki basamaklı bir asal sayıdır.
▇’nin yerine yazılabilecek doğal sayıların toplamını bulunuz.
Cevap:
Çift basamaklı bir sayı olamaz bu yüzden geriye çift olmayan ve 5 ile başlayan sayılardan 51, 53, 55, 57 ve 59 kalır.
51 ve 57 3’e bölünebilir. 55 ise 5’e bölünebilir.
Bu yüzden sayımız 53 veya 59’dur. Yani ▇ yerine yalnızca 3 ve 9 yazılabilir.
3 + 9 = 12 yapar.
Örnek 4
77 doğal sayısının en büyük asal çarpanı ile en küçük asal çarpanı arasındaki farkı bulunuz.
Cevap:
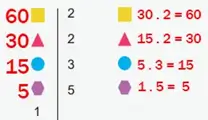
Örnek 5
Yandaki asal çarpan algoritmasında sembollerin temsil ettiği doğal sayıları bulunuz.
Cevap:

Örnek 6
Yandaki çarpan ağacında sembollerin temsil ettiği doğal sayıların toplamını bulunuz.
Cevap:

6. Sınıf Matematik Ders Kitabı Sayfa 46 Cevapları MEB Yayınları
Etkinlik 5: Numaram Asal Sayı Mı?
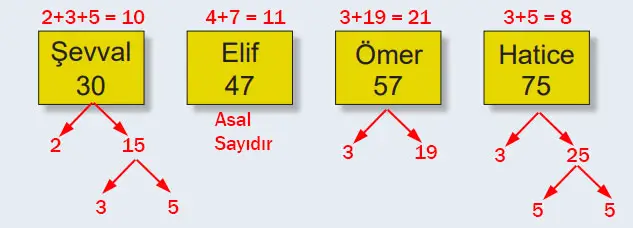
1) Oyunun sonunda en fazla puana ulaşan öğrenciyi belirleyiniz.
Cevap: En fazla puana 21 puan ile Ömer ulaşabilmiştir.
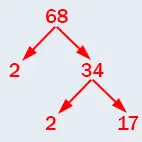
2) Oyuna okul numarası 68 olan bir öğrenci katılırsa oyunun sonunda en fazla puan alan öğrenci değişir mi? Fikirlerinizi arkadaşlarınızla paylaşarak tartışınız.
Cevap: 2+17 = 19 yapar. Bu da yine 21’i geçemeyeceği için hala Ömer en fazla puana sahip olmuş olur.
6. Sınıf Matematik Ders Kitabı Sayfa 47 Cevapları MEB Yayınları
Performans Görevi
“Erathosthenes Kalburu Tasarımı”
Bu çalışmada “Erathosthenes (Eratosten) Kalburu” ile ilgili araştırma yaparak ulaştığınız bilgileri panoda sergilemeniz ve “Erathosthenes Kalburu” tasarımı yapmanız beklenmektedir. Yapacağınız araştırmada güvenilir bilgiye ulaşma yollarını belirlemeniz ve özgün tasarımlar oluşturmanız önemlidir.
Cevap: Erathosthenes (Eratosten) Kalburu MÖ 3. yüzyılda Yunan matematikçi Eratostenes tarafından geliştirilmiş antik bir yöntemdir
Eratosten Kalburuna göre belli bir sayıya kadar olan asal sayıları bulabilmek için başvurulan basit bir yöntemdir. Belirli boşluktaki tüm sayıları bir araya getirip, asal olmayan sayıları belirleyerek kullanılır. Bu yöntem bir çok matematik formülünde ve bilgisayar çalışma prensibinde kullanılmıştır. Prensip şu şekilde çalışır:
- Öncelikle, belirlenen sınıra kadar olan tüm tam sayılar bir liste halinde yazılır. Örneğin, 2’den 100’e kadar olan sayılar.
- Listenin ilk sayısı olan 2 en küçük asal sayısı baz alınır.
- 2’nin katları olan tüm sayılar listeden silinir. Çünkü 2’nin katları asal olamaz.
- Listede kalan bir sonraki sayı 3 baz alınır.
- 3’ün katları olan tüm sayılar listeden silinir.
- Bu işlem 5, 7, 11 gibi diğer asal sayılar için yapılır.
Geriye kalan sayılar asal sayı olacaktır.
Aradığınız ödevi bulamadıysanız lütfen MEB Yayınları 2025 ana içeriğimizi ziyaret ediniz.
Ders ve Çalışma kitabı cevapları aramalarınızda internet sitemizi daha üst sıralarda listelemek için aramalarınızın sonuna "forum sınıf" yazabilirsiniz.
Örnek Kullanım: 3. sınıf türkçe sayfa 11 forum sınıf

